[next] [prev] [prev-tail] [tail] [up]

G Transform gyrokinetic equation from (X,μ,𝜀,α) to (X,μ,v∥,α) coordinates

The gyrokinetic equation given above is written in terms of variables (X,μ,𝜀,α). Next, we transform it into coordinates (X′,μ′,v∥,α′) which are defined by

( || X′ = X { μ′ = μ || α′ = α∘------------- ( v∥ = σ 2(𝜀− μB0(X ))
(377)

Use this definition and the chain rule, we obtain

| -∂-|| = ∂X-′⋅-∂--+ ∂μ-′∂--+ ∂v∥ ∂--+ ∂α-′∂-- ∂X |μ,𝜀,α ∂X ∂X ′ ∂X ∂μ′ ∂X ∂v∥ ∂X ∂α′ ∂ μ ∂B0 ∂ = ∂X-′ − v-∂X-∂v-, (378) ∥ ∥

and

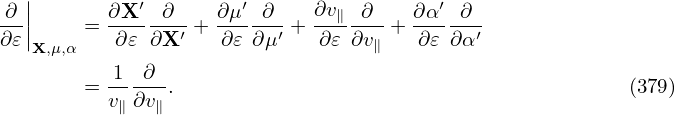
|| ′ ′ ∂v ′ ∂-|| = ∂X---∂′ + ∂μ--∂′ +--∥ -∂-+ ∂-α -∂′ ∂𝜀 X,μ,α ∂𝜀 ∂X ∂𝜀 ∂μ ∂𝜀 ∂v∥ ∂𝜀 ∂α = 1--∂-. (379) v∥∂v∥

Then, in terms of (X′,μ′,v∥,α′), equation (135) is written

[ ∂ ∂ ] μ∂B0 ∂δG0 ∂t + (v∥e∥ + VD + δVD )⋅∂X-′ δG0 − (v∥e∥ + VD + δVD )⋅v-∂X--∂v-- ( ) ∥ ∥ = − δVD ⋅ ∂F0-− μ-∂B0-∂F0- − -q ∂⟨δL-⟩α-∂F0-1-, (380) ∂X ′ v∥∂X ∂v∥ m ∂t ∂v∥ v∥

Dropping terms of order higher than O(λ2), equation (380) is written as

[ ] ∂- -∂-- ∂B0-∂δG0- ∂t + (v∥e∥ + VD + δVD )⋅∂X ′ δG0 − e∥ ⋅μ∂X ∂v∥ (∂F0 ) ( ∂B0 q ∂⟨δL⟩α) ∂F0 1 = − δVD ⋅ ∂X-′ + δVD ⋅μ ∂X--− m---∂t-- ∂v--v-, (381) ∥ ∥

The above equation drops all terms higher than O(λ2) and as a result the coefficient before ∂δf∕∂v∥ contains only the mirror force, i.e., −e∥⋅ μ∇B0, which is independent of any perturbations.

Note that the gyro-averaging operator in (X′,μ′,v∥,α′) coordinates is identical to that in the old coordinates since the perpendicular velocity variable μ is identical between the two coordinate systems. Also note that the perturbed guiding-center velocity δVD is given by

e∥-×∇X-⟨δϕ⟩α ⟨δB-⊥⟩α- δVD = B0 + v∥ B0 ,
(382)

where ∂∕∂X (rather than ∂∕∂X′) is used. Since δϕ(x) = δϕg(X,μ′,α′), which is independent of v∥, then Eq. (378) indicates that ∂δϕ∕∂X = ∂δϕ∕∂X′.

Following the same procedures, equation (143) in terms of (X′,μ′,v∥,α′) is written as

[ ∂ ∂ ] ∂δf --+ (v∥e∥ + VD + δVD )⋅---′ δf − e∥ ⋅μ∇B0---- ∂t ( ) ∂X ∂v∥ = − δVD ⋅ ∂F0- + δVD ⋅μ ∇B0 ∂F0-1 ∂X ′ ∂v∥v∥ q [ ∂⟨v⋅δA ⟩α ( ⟨δB⊥ ⟩α ) ] ∂F0 1 − m- − ----∂t---− v∥e∥ + VD + v∥-B0--- ⋅∇X ⟨δϕ⟩α ∂v∥v∥. (383)

next, try to recover the equation in Mishchenk’s paper:

[ ∂ ∂ ] ∂δf -- + (v∥e∥ + VD + δVD )⋅---′ δf − e∥ ⋅μ∇B0---- ∂t ( ) ∂X ∂v∥ = − δV ⋅ -∂F0 + δV ⋅μ∇B ∂F0-1- D ∂X ′ D 0∂v ∥v∥ q [ ∂⟨δA ∥⟩α ( VD ⟨δB ⊥⟩α) ] ∂F0 − m- − --∂t---− e∥ +-v--+ --B---- ⋅∇X ⟨δϕ⟩α ∂v--. ∥ 0 ∥

δL = δΦ − v ⋅ δA,

δVD- --q- e∥ v∥ = −mv ∥∇X ⟨δΦ− v∥A ∥⟩α × Ω .
(384)

[ ( ) ] −-q − ∂⟨δA∥⟩α − e∥ + VD-+ -q∇X ⟨A∥⟩α × e∥ ⋅∇X ⟨δϕ⟩α ∂F0. m ∂t v∥ m Ω ∂v∥

[ (h) ( ) ] − -q − ∂⟨δA∥--⟩α-− VD--+ -q∇ ⟨A ⟩ × e∥ ⋅∇ ⟨δϕ⟩ ∂F0. m ∂t v∥ m X ∥ α Ω X α ∂v∥

 

G.1 Recover equation in W. Deng’s 2011 NF paper

The guiding-center velocity in the equilibrium field is given by

⋆ v∥e∥ + VD = -B0⋆-v∥ +--μ⋆-B0 × ∇B0 + --1-⋆-E0 × B0 B ∥0 ΩB ∥0 B0B ∥0
(385)

where

⋆ v∥ B0 = B0 + B0 Ω ∇ × b,
(386)

⋆ ⋆ ( v∥ ) B ∥ ≡ b ⋅B = B 1+ Ω b ⋅∇ × b ,
(387)

Using B∥0⋆ ≈ B0, then expression (385) is written as

v2∥ --μ- -1- v∥e∥ + VD = v∥b + Ω-∇ ×-b + ΩB0 B0 × ∇B0 + B20E0 × B0, cu◟rva◝t◜ured◞rift ◟---∇B◝◜drift--◞ ◟---◝◜---◞ E×B drift
(388)

where the curvature drift, ∇B drift, and E0 × B0 drift can be identified. Note that the perturbed guiding-center velocity δVD is given by (refer to Sec. C.3)

e∥-×∇X-⟨δϕ⟩α ⟨δB-⊥⟩α- δVD = B0 + v∥ B0 .
(389)

Using the above results, equation (383) is written as

[ ∂ ∂ ] ∂δf ∂t +(v∥e∥ + VD + δVD )⋅∂X-′ δf − e∥ ⋅μ ∇B0 ∂v ( ) ( ) ∥( ) = − δVD ⋅ ∂F0- + e∥-×∇X-⟨δϕ⟩α + v∥⟨δB-⊥⟩α- ⋅ μ-∇B0 ∂F0- ∂X ′ B0 B0 v∥ ∂v∥ q [ ∂⟨v ⋅δA ⟩ ( v2 μ 1 ⟨δB ⟩ ) ] ∂F 1 − -- − -------α-− v∥e∥ + -∥∇ × b+ ---- B0 × ∇B0 + -2E0 × B0 + v∥---⊥-α- ⋅∇X ⟨δϕ ⟩α --0(390), m ∂t Ω ΩB0 B0 B0 ∂v∥ v∥

Collecting coefficients before ∂F0∕∂v∥, we find that the two terms involving ∇B0 (terms in blue and red) cancel each other, yielding

[ ] ∂- +(v∥e∥ + VD + δVD )⋅-∂-′ δf − e∥ ⋅μ ∇B0 ∂δf ∂t ( ) ∂X ∂v∥ = − δV ⋅ ∂F0- D ∂X [ ( v2 ) ] + q- m-v∥⟨δB⊥-⟩α-⋅(μ∇B0 )+ ∂⟨v-⋅δA-⟩α + v∥b+ ∥-∇ ×b + -12E0 × B0 + v∥⟨δB-⊥⟩α ⋅∇X ⟨δϕ ⟩α ∂F0(3191,) m q B0 ∂t Ω B 0 B0 ∂v∥ v∥

This equation agrees with Eq. (8) in I. Holod’s 2009 pop paper (gyro-averaging is wrongly omitted in that paper) and W. Deng’s 2011 NF paper.

 

 

[next] [prev] [prev-tail] [front] [up]