[prev] [prev-tail] [tail] [up]

3.6 Equation for the non-adiabatic part δG

Plugging expression (94) into Eq. (82), we obtain

q [ e∥] ∂Fg0 q ∂δL∂Fg0 LgδG = − m- (− ∇X ⊥ δL− v⊥ ⋅∇X ⊥δA )× Ω ⋅∂X--− m-∂t--∂-𝜀 + δRδFg,
(95)

where Lg is given by Eq. (73), i.e.,

Lg = -∂ + (v∥e∥ + VE0 )⋅-∂ + v⋅[λB1 + λB2 ]− Ω-∂ ∂t ( ∂X ) ∂ α + -qE0 ⋅ v-⊥-∂-+ eα--∂- , (96) m B0 ∂μ v⊥ ∂α
Expansion of δG

Expand δG as

δG = δG0 + δG1 + …,

where δGi ∼ O(λi+1)Fg0, and note that the right-hand side of Eq. (95) is of O(λ2), then, the balance on order O(λ1) requires

∂-δG0- ∂ α = 0,
(97)

i.e., δG0 is gyro-phase independent.

The balance on order O(λ2) requires (for the special case of E0 = 0):

∂δG0-+ v∥e∥ ⋅ ∂δG0-+ v ⋅[λB1 + λB2]δG0 ∂t [ ∂X ] = −-q (− ∇X ⊥δL − v⊥ ⋅∇X δA )× e∥ ⋅ ∂Fg0 − q-∂δL-∂Fg0+ δR δFg. (98) m Ω ∂X m ∂t ∂𝜀
Gyro-averaging

Define the gyro-average operator ⟨…⟩α by

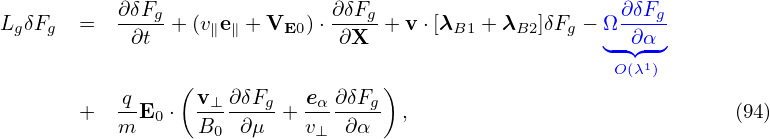− 1∫ 2π ⟨h⟩α = (2π) hdα, 0
(99)

where h = h(X,α,𝜀,μ) is an arbitrary function of guiding-center variables. The gyro-averaging is an integration in the velocity space. [For a field quantity, which is independent of the velocity in particle coordinates, i.e., h = h(x), it is ready to see that the above averaging is a spatial averaging over a gyro-ring.]

Gyro-averaging Eq. (98), we obtain

∂δG0 ⟨ ∂ δG0 ⟩ -∂t--+ v∥e∥ ⋅-∂X- + ⟨v⋅[λB1 + λB2 ]δG0⟩α [ e ] = −-q − ∇X ⊥⟨δL⟩α ×-∥ ⋅ ∂Fg0 − q-∂⟨δL⟩α∂Fg0 + ⟨δRδFg⟩α, (100) m Ω ∂X m ∂t ∂𝜀
where use has been made of ⟨(v⊥⋅∇X)δA⟩α ≈ 0, where the error is of order higher than O(λ2). Note that v∥ = ±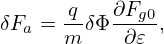∘ ---------- 2(𝜀− B0μ ). Since B0 is approximately independent of α, so does v∥. Using this, the first gyro-averaging on the left-hand side of the above equation is written
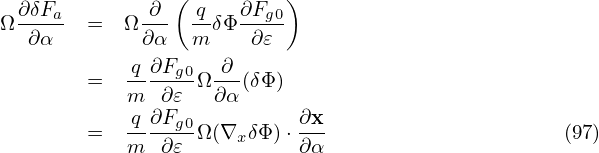⟨ ⟩ ∂δG0- ∂δG0- ∂δG0- v∥e∥ ⋅ ∂X α = ⟨v∥e∥⟩⋅ ∂X = v∥e∥ ⋅ ∂X
(101)

The second gyro-averaging on the left-hand side of Eq. (100) can be written as

⟨v ⋅[λB1 + λB2]δG0⟩α = VD ⋅∇X δG0,
(102)

where VD is the magnetic curvature and gradient drift (Eq. (102) is derived in Appendix xx, to do later). Then Eq. (100) is written

[ ∂ ] ∂t + (v∥e∥ + VD )⋅∇X δG0 [ ] = −-q − ∇X ⊥⟨δL⟩α × e∥ ⋅ ∂Fg0 − q-∂⟨δL⟩α ∂Fg0+ ⟨δRδFg⟩α. (103) m Ω ∂X m ∂t ∂𝜀
Simplification of the nonlinear term

Next, we try to simplify the nonlinear term ⟨δRδFg⟩α appearing in Eq. (103), which is written as

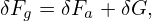
⟨ ( ) ⟩ ⟨δRδFg⟩α = δR -qδΦ ∂Fg0+ δG0 ⟨ m( ∂𝜀 )⟩ α -q ∂Fg0 = m δR δΦ ∂𝜀 α + ⟨δRδG0⟩α (104)
First, let us focus on the first term, which can be written as
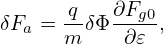
( ) ( ) ( ) ( ) ( ) δR δΦ ∂Fg0 ≈ − q-∂Fg0 δE + v×-δB- × e∥ ⋅ ∂δΦ-− q-∂Fg0 v-×-δB ⋅ eα-∂δΦ- ∂𝜀 m ∂𝜀 ( c Ω ∂X ) m ∂𝜀 c v⊥ ∂α -q∂Fg0 ∂δΦ- v⊥-∂δΦ- eα-∂δΦ- -q ∂2Fg0 − m ∂ 𝜀 δE⋅ v ∂𝜀 + B0 ∂μ + v⊥ ∂ α + m δΦδE ⋅v ∂𝜀2 q ( v × δB) q ∂2F = − -- δE + ------ ⋅∇v δΦ+ -δΦ δE⋅v ---g20 m c m ∂𝜀 = -qδΦδE ⋅v ∂2Fg0- (105) m ∂ 𝜀2
Using the above results, the nonlinear term ⟨δRδF⟩α is written as
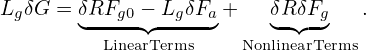q ⟨ ∂2F ⟩ ⟨δRδF ⟩α = -- δΦδE ⋅v---g20 + ⟨δRδG0⟩α m ∂𝜀 α
(106)

Accurate to O(λ2),the first term on the right-hand side of the above is zero. [Proof:

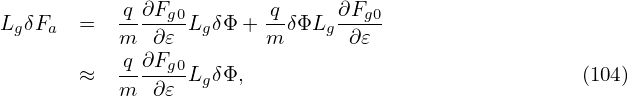
⟨ ∂2Fg0⟩ ⟨ ∂2Fg0 ⟩ δΦ δE ⋅v -∂𝜀2- = -∂𝜀2-δΦ∇ δΦ ⋅v α 2 α = ∂-Fg0⟨v ⋅∇(δΦ)2⟩α ∂𝜀2 ≈ ∂2Fg0⟨v ⋅∇(δΦ)2⟩ ∂𝜀2 ⊥ α ≈ 0, (107)
where use has been made of ⟨v⊥⋅∇XδΦ⟩α ≈ 0, where the error is of O(λ2). Using the above results, expression (106) is written as
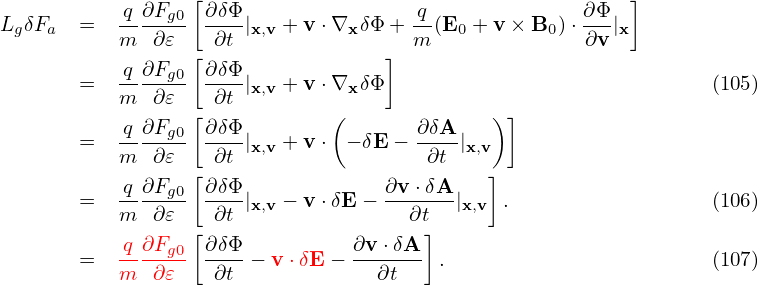⟨δRδFg⟩α = ⟨δR δG0⟩α.
(108)

Using the expression of δR given by Eq. (37), the above expression is written as

⟨( ) ( )⟩ ⟨δRδG ⟩ = −-q δE + v-×-δB × e∥ ⋅ ∂δG0 0α m c Ω α ∂X q ∂δG0 q∂ δG0 ⟨ v⊥⟩ −m- -∂𝜀-⟨δE ⋅v⟩α − m-∂-μ- δE ⋅B0- (109) α
where use has been made of ∂δG0∕∂α = 0. Using Eq. (92), we obtain
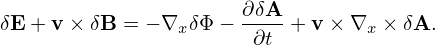q ⟨ ( e∥)⟩ q e∥ − m- (δE +v × δB) × Ω- α = m-∇X ⊥⟨δL⟩α × Ω-.
(110)

The other two terms in Eq. (109) can be proved to be zero. [Proof:

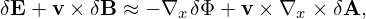
q∂δG0 q∂ δG0 −m---∂𝜀-⟨δE ⋅v ⟩α = m---∂𝜀-⟨v⋅∇x Φ⟩α q∂ δG0 ≈ m---∂𝜀-⟨v⊥ ⋅∇xΦ⟩α q∂ δG0 ≈ m---∂𝜀-⟨v⊥ ⋅∇X Φ⟩α ≈ 0 (111)
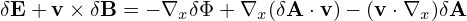
⟨ ⟩ ⟨ ⟩ − -q∂δG0- δE⋅ v⊥- = q-∂δG0- -1-v ⋅∇ Φ m ∂μ B0 α m ∂μ B0 ⊥ x α q ∂δG0 ⟨ 1 ⟩ ≈ m--∂μ-- B0-v⊥ ⋅∇X Φ α ≈ 0 (112)
] Using the above results, the nonlinear term is finally written as
-q[ e∥] ⟨δRδG0 ⟩α = m ∇X ⊥⟨δL⟩α × Ω ⋅∇X δG0.
(113)

Using this in Eq. (108), we obtain

[ ] ⟨δRδFg⟩α = q- ∇X ⊥⟨δL⟩α × e∥ ⋅∇X δG0, m Ω
(114)

which is of O(λ2).

Final equation for the non-adiabatic part of the perturbed distribution function

Using the above results, the gyro-averaged kinetic equation for δG0 is finally written as

( ) ∂δG0-+ || v e + VD − -q∇X ⟨δL⟩α × e∥|| ⋅∇X δG0 ∂t ( ∥ ∥ m◟------◝◜----Ω◞) nonlinear (-q e∥) q-∂⟨δL⟩α∂Fg0 = m ∇X ⟨δL⟩α × Ω ⋅∇XFg0 − m ∂t ∂𝜀 . (115) ◟------spati◝al◜−-drive------◞ v◟elocit− s◝p◜ace−-dam◞p
where VD is the equilibrium guiding-center drift velocity, ⟨…⟩α is the gyro-phase averaging operator, δL = δΦ− v ⋅δA, and δG0 = δG0(X,𝜀,μ,t) is gyro-angle independent and is related to the perturbed distribution function δFg by
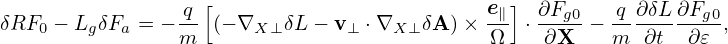q ∂F δFg = --δΦ---g0+ δG0, m ∂ 𝜀
(116)

where the first term is called “adiabatic term”, which depends on the gyro-phase α via δΦ. Equation (115) is the special case (∂Fg0∕∂μ|𝜀 = 0) of the Frieman-Chen nonlinear gyrokinetic equation given in Ref. [3]. Note that the nonlinear terms only appear on the left-hand side of Eq. (115) and all the terms on the right-hand side are linear. The term

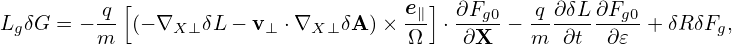− q-∇X ⟨δL⟩α × e∥, m Ω
(117)

consists of the perturbed E × B drift and magnetic fluttering term (refer to Sec. E.3).

[prev] [prev-tail] [front] [up]